Question

PLEASE HELP!!!!

On top of a hill, a rocket is launched from a distance 80 feet above a lake. The rocket will fall into the lake after its engine burns out. The rocket's height, h, in feet above the surface of the lake, is given by the equation, h = -16t ∧2 + 64t + 80, where t is time in seconds. The maximum height of the rocket is ______ feet.

Answer 1

144

Explanation:

`h=-16t^2+64t+80`

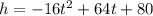
So you have to figure out which number t results in the maximum h.

First find the range.

`64t+80>16t^2`

`4t+5>t^2`

`t^2-4t-5<0`

`(t-5)(t+1)<0`

`t<5, t>-1`

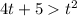
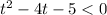
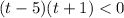
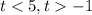
It looks like t has to be less than 5 and greater than -1 to be positive.

Now just try the numbers 0, 1, 2, 3, 4

0: 80

1: 128

2: 144

3: 128

4: 80

Answer 2

144 ft

Explanation:

h = -16t ^2 + 64t + 80,

We want to find the maximum height or the vertex

This occurs when at

t = -b/2a

t = -64/ (2(-16)

= -64/-32 = 2

When t=2

h(2) = -16 (2)^2 +64(2) +80

= -16*4+128 +80

=-64 +128 +80

=144

h(2) = 144

The maximum height is 144