Question

Assignment: The Discriminant

Part I: Practice Finding the Discriminant
Find the value of the discriminant for each quadratic equation below. Show all steps needed to
write the answer in simplest form, including substituting the values of a, b, and cin the
discriminant formula. Then use the value to determine how many real number solutions each
equation has.
1.
x + 6x-3.0
2. 3x + 2x+1=0
3. x + 4x + 4 = 0
4. 5x + x = 4
5. 2x -3x = -5
6.
X-X=12

Answer 1

1. D = 48, two; 2. D = -8, none; 3. D = 0, one

4.D = 81, two; 5. D = -91, none; 6. D = 49, two

Explanation:

The formula for a quadratic equation is

ax² + bx + c = 0

The quadratic formula gives the roots:

`x = (-b\pm√(b^2-4ac))/(2a) = (-b\pm√(D))/(2a)`

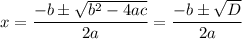
D is the discriminant.

It tells us the number of roots to the equation — the number of times the graph crosses the x-axis.

`D = \begin{cases}\text{positive} & \quad \text{2 real solutions}\\\text{zero} & \quad \text{1 real solution}\\\text{negative} & \quad \text{0 real solutions}\\\end{cases}`

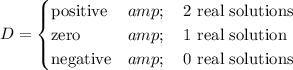
It doesn't matter if the graph opens upwards or downwards.

If D > 0, the graph crosses the x-axis at two points.

If D = 0, the graph touches the x-axis at one point.

If D < 0, the graph never reaches the x-axis.

1. x² + 6x - 3 =0

a= 1; b = 6; c= -3

D = b² - 4ac = 6² - 4×1×(-3) = 36 - 4(-3) = 36 + 12 = 48

D > 0: two real solutions

2. 3x² + 2x + 1 = 0

a = 3; b = 2; c =1

D = b² - 4ac = 2² - 4×3×1 = 4 - 12 = -8

D < 0: no real solutions

3. x² + 4x + 4 = 0

a = 1; b = 4; c =1

D = 4² - 4×1×4 = 16 - 16 = 0

D = 0: one real solution

4. 5x² + x = 4

5x² + x - 4 = 0

a = 5; b = 4; c = -4

D = 1² - 4×5×(-4) = 1 - 20(-4) = 1 - (-80) = 1 + 80 = 81

D > 0: two real solutions

5. 5x² - 3x = -5

5x² - 3x + 5= 0

a = 5; b = -3; c = 5

D = (-3)² - 4×5×5 = 9 - 100 = -91

D < 0: no real solutions

6. x² - x = 12

x² - x - 12= 0

a = 1; b = 1; c = -12

D = 1² - 4×1×(-12) = 1 - 4(-12) = 1 + 48 = 49

D > 0: two real solutions