Answer:
1. D = 48, two; 2. D = -8, none; 3. D = 0, one
4.D = 81, two; 5. D = -91, none; 6. D = 49, two
Explanation:
The formula for a quadratic equation is
ax² + bx + c = 0
The quadratic formula gives the roots:
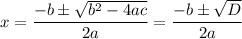
D is the discriminant.
It tells us the number of roots to the equation — the number of times the graph crosses the x-axis.

It doesn't matter if the graph opens upwards or downwards.
If D > 0, the graph crosses the x-axis at two points.
If D = 0, the graph touches the x-axis at one point.
If D < 0, the graph never reaches the x-axis.
1. x² + 6x - 3 =0
a= 1; b = 6; c= -3
D = b² - 4ac = 6² - 4×1×(-3) = 36 - 4(-3) = 36 + 12 = 48
D > 0: two real solutions
2. 3x² + 2x + 1 = 0
a = 3; b = 2; c =1
D = b² - 4ac = 2² - 4×3×1 = 4 - 12 = -8
D < 0: no real solutions
3. x² + 4x + 4 = 0
a = 1; b = 4; c =1
D = 4² - 4×1×4 = 16 - 16 = 0
D = 0: one real solution
4. 5x² + x = 4
5x² + x - 4 = 0
a = 5; b = 4; c = -4
D = 1² - 4×5×(-4) = 1 - 20(-4) = 1 - (-80) = 1 + 80 = 81
D > 0: two real solutions
5. 5x² - 3x = -5
5x² - 3x + 5= 0
a = 5; b = -3; c = 5
D = (-3)² - 4×5×5 = 9 - 100 = -91
D < 0: no real solutions
6. x² - x = 12
x² - x - 12= 0
a = 1; b = 1; c = -12
D = 1² - 4×1×(-12) = 1 - 4(-12) = 1 + 48 = 49
D > 0: two real solutions