Answer:
Difference in the length of AB and AD will be 1.17 units
Explanation:
From the figure attached,
In ΔABC and ΔADC,
x = 45°
y = 63°
AC = 4 units
By applying Sine rule in ΔABC,
SinB =
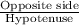
Sin(x) =
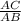
Sin(45)° =
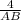
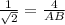
AB = 4√2 ≈ 5.657 units
Similarly, by applying sine rule in ΔADC,
Sin(y)° =

Sin(63)° =
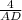
AD =
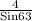
= 4.489 units
AB - AD = 5.657 - 4.489
= 1.168
≈ 1.17 units
Therefore, difference in the length of AB and AD will be 1.17 units