Question

Given ΔQXY with RS || XY Prove XR/RQ = YS/SQ statements: 1. RS || XY 2. ∠1=∠3, ∠2=∠4 3. ΔQXY ~ΔQRS 4. XQ/RQ = YQ/SQ 5. XQ=XR+RQ, YQ=YS+SQ 6. XR+RQ/RQ = YS=SQ/SQ 7. XR/RQ = YS/SQ

Answer 1

It can be proved by:

The two triangles are similar and the ratio of corresponding sides are equal.

Explanation:

We are given a ΔQXY which has a line RS inside it such that RS || XY.

To prove:

`(XR)/(RQ) = (YS)/(SQ)`

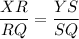
First of all, let us have a look at the ΔQXY and ΔQRS as per the given question figure:

1. ∠1=∠3 (Because sides XY || RS and ∠1, ∠3 are corresponding angles)

2. ∠2=∠4 (Because sides XY || RS and ∠2, ∠4 are corresponding angles)

3. ∠Q is common to both the triangles.

So, all the three angles are equal to each other, hence the two triangles are similar:

`\triangle QXY \sim \triangle QRS`

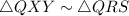
If two triangles are similar, then ratio of their corresponding sides is also equal.

`(XQ)/(RQ) = (YQ)/(SQ)`

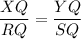
Subtracting 1 from both the sides:

`(XQ)/(RQ) -1= (YQ)/(SQ)-1\\(XQ-RQ)/(RQ)= (YQ-SQ)/(SQ)`

Now, it is clearly observable that:

XQ - RQ = XR and

YQ - SQ = YS

Putting the values in above equation:

`(XR)/(RQ) = (YS)/(SQ)`

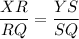
Hence proved.