Answer:
The diagram is attached below.
Explanation:
A normal distribution mean 0 and standard deviation 1 is known as the standard normal distribution.
So, the readings on the thermometers (denoted by Z) follows N (0, 1).
It is provided that 2.7% of the thermometers are rejected because they have readings that are too high and 2.7% are rejected because they have readings that are too low.
This implies that:
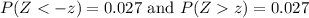
The value of z associated to both these probabilities are:
z = 1.93.
That is,
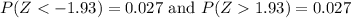
*Use a z-table.
The diagram for the two readings that are cutoff values separating the rejected thermometers from the others is attached below.