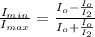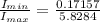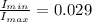Answer:
The ratio is
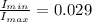
Step-by-step explanation:
Let assume that the intensity of the unpolarized photon beam is
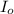
The through the linear polarizer is mathematically represented as

Here
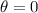 given that the polarizer is linear
given that the polarizer is linear
So
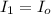
The intensity of the
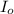 emerging from the polarizer oriented 45° to the horizontal is
emerging from the polarizer oriented 45° to the horizontal is
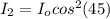
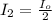
The maximum photon probability density is mathematically represented as
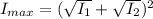
=>

The minimum photon probability density is mathematically represented as
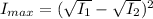

The ratio of minimum to maximum is mathematically represented as