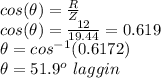Question

. A series RLC circuit containing a resistance of 12Ω, an inductive reactance of 47.13 Ω and a capacitive reactance of 31.83 Ω are connected in series across a 100V, 50Hz supply. Calculate the

Answer 1

a) 19.44 ohm

b) 5.14 A

c) 51.9° lagging

Step-by-step explanation:

A series RLC circuit containing a resistance of 12Ω, an inductive reactance of 47.13 Ω and a capacitive reactance of 31.83 Ω are connected in series across a 100V, 50Hz supply. Calculate the total circuit impedance, the circuits current, power factor

Given that:

R = 12 Ω,
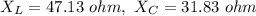`X_L=47.13\ ohm,\ X_C=31.83 \ ohm`, f = 50 Hz,

A) Total circuit impedance (Z) is given by:

`Z=√(R^2+(X_L-X_C)^2) =√(12^2+(47.13^2-31.83)^2) =√(378.09) =19.44\ ohm`

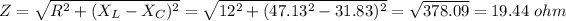
B) the circuits current (I) is given by:

`I=(V)/(Z)=(100)/(19.44)=5.14\ A`

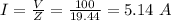
The voltage across the resistor (
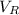`V_R`) = IR= 5.14 × 12 = 61.68 V

The voltage across the inductor (
`V_L`) =
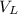`IX_L` = 5.14 × 47.13 = 242.25 V

The voltage across the capacitor (
`V_c`) =
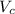`IX_C` = 5.14 × 31.83 = 163.5 V

C) The power factor (Θ) is calculated as:

`cos(\theta)=(R)/(Z)\\cos(\theta)=(12)/(19.44) =0.619\\\theta=cos^(-1)(0.6172)\\\theta=51.9^o\ laggin`