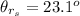Question

Three sheets of plastic have unknown indices of refraction. Sheet 1 is placed on top of sheet 2, and a laser beam is directed onto the sheets from above so that it strikes the interface at an angle of 26.50 with the normal. The refracted beam in sheet 2 makes an angle of 31.70 with the normal. The experiment is repeated with sheet 3 on top of sheet 2, and with the same angle of incidence, the refracted beam makes an angle of 36.70 with the normal. If the experiment is repeated again with sheet 1 on top of sheet 3, determine the expected angle of refraction in sheet 3? Assume the same angle of incidence.

Answer 1

The angle of refraction of sheet 3 when sheet 1 is on top of it is
`\theta_(r_s ) = 23.1 ^o`

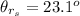
Step-by-step explanation:

From the question we are told that

The angle of incidence is
`\theta _i = 26.50 ^o`

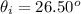
The angle of refraction angle for sheet 1 is
`\theta _(r_1)} = 31.70 ^o`

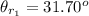
The angle of refraction for sheet 3 is
`\theta _(r_3)} = 36.70 ^o`

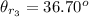
According to Snell's law

`(n_2)/(n_1) = (sin (\theta_1))/(sin (\theta_(r_1)))`

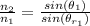
Where
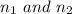`n_1 \ and \ n_2` are refractive index of sheet 1 and sheet 2

=>
`n_2 = n_1 (sin(\theta_i))/(sin (\theta _(r_1)))`

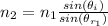
Also when sheet 3 in on top of sheet 2

`(n_2)/(n_3) = (sin \theta_i)/(sin \theta_(r_3))`

substituting for
`n_2`

`n_1 (sin(\theta_i))/(sin (\theta _(r_1))) = n_3 (sin \theta_i)/(sin \theta_(r_3))`

`n_1 (sin(\theta_i))/(sin (\theta _(r_1))) = n_3 (sin \theta_i)/(sin \theta_(r_3))`

=>
`n_3 = n_1 * (sin(\theta_(r_3)))/(sin(\theta_(r_1)))`

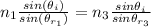
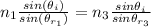
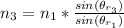
when sheet 1 in on top of sheet 3

`(n_3)/(n_1) = (sin(\theta_i))/(\theta_(r_s))`

where
`r_s` is the angle of refraction when sheet 1 is on top of sheet 3

substituting for
`n_3`

`( n_1 * (sin(\theta_(r_3)))/(sin(\theta_(r_1))))/(n_1) = (sin(\theta_i))/(\theta_(r_s))`

=>
`sin (\theta _(r_s)) = n_1 * sin (\theta_i) * (sin (\theta_(r_1)))/( n_1 * sin(\theta_(r_3)))`

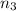
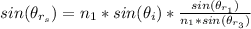
substituting values

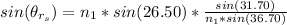
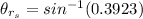
`sin (\theta _(r_s)) = n_1 * sin (26.50) * (sin (31.70))/( n_1 * sin(36.70))`

=>
`\theta_(r_s ) = sin^(-1) (0.3923)`

=>
`\theta_(r_s ) = 23.1 ^o`