Answer:
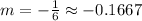
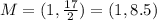
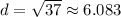
Explanation:
(i) For two different points on a line, the slope m is defined as the difference on the y-axis divided by the difference on the x-axis:
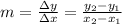
Where:

So:
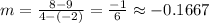
(ii)
To find the coordinates of the midpoint, you can use the following formula:
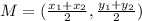
Therefore:
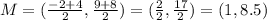
(iii) The distance between two points is given by the following formula:

Hence:
