Answer:
a)
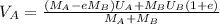
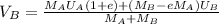
b)
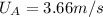
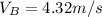
c) Impulse = 0 kg m/s²
d) percent decrease in kinetic energy = 47.85%
Step-by-step explanation:
Let
 be the initial velocity of rod A
be the initial velocity of rod A
Let
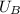 be the initial velocity of rod B
be the initial velocity of rod B
Let
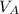 be the final velocity of rod A
be the final velocity of rod A
Let
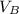 be the final velocity of rod B
be the final velocity of rod B
Using the principle of conservation of momentum:
 ............(1)
............(1)
Coefficient of restitution,

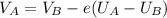 ........................(2)
........................(2)
Substitute equation (2) into equation (1)
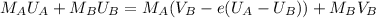 ..............(3)
..............(3)
Solving for
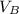 in equation (3) above:
in equation (3) above:
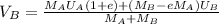 ....................(4)
....................(4)
From equation (2):
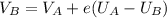 ......(5)
......(5)
Substitute equation (5) into (1)
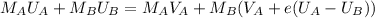 ..........(6)
..........(6)
Solving for
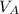 in equation (6) above:
in equation (6) above:
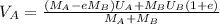 .........(7)
.........(7)
b)
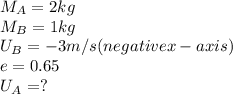
Rod A is said to be at rest after the impact,
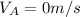
Substitute these parameters into equation (7)
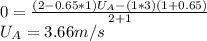
To calculate the final velocity,
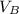 , substitute the given parameters into (4):
, substitute the given parameters into (4):
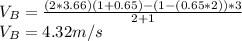
c) Impulse,
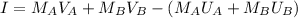
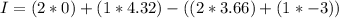
I = 0
d) %
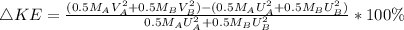
%
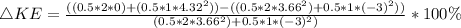
%
