Question

Suppose that the operations manager of a nose mask packaging delivery service is

contemplating the purchase of a new fleet of trucks. When

packages are efficiently stored in the trucks in preparation for delivery, two major constraints

have to be considered. The weight in pounds and volume in cubic feet for each item. Now

suppose that in a sample of 200 packages the average weight is 26.0 pounds with a standard

deviation of 3.9 pounds. In addition suppose that the average volume for each of these

packages is 8.8 cubic feet with standard deviation of 2.2 cubic feet. How can we compare the

variation of the weight and volume?​

Answer 1

Coefficient of variation (weight) = 15%

Coefficient of variation (volume) = 25%

Explanation:

Let's begin by listing out the given information:

Population = 200, Average weight = 26 lb,

standard deviation (weight) = 3.9 lb,

Average volume = 8.8 ft³,

standard deviation (volume) = 2.2 ft³

Based on the data given, the manager will have to make a deduction by comparing the relative scatter of both variables due to the different units of measuring weight (pounds) and volume (cubic feet).

To compare the variation of the weight and volume, we use the coefficient of variation given by the formula:

Coefficient of Variation = (Standard deviation ÷ Mean) * 100%

⇒
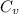`C_(v)` = (σ ÷ μ) * 100%

For weight

σ = 3.9 lb, μ = 26 lb

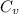`C_(v)` (weight) = (3.9 ÷ 26.0) * 100% = 15%

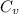`C_(v)` (weight) = 15%

For volume

σ = 2.2 ft³, μ = 8.8 ft³

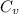`C_(v)` (volume) = (2.2 ÷ 8.8) * 100% = 25%

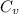`C_(v)` (volume) = 25%

∴ the relative variation of the volume of the package is greater than that of the weight of the package