Question

Please give me concept to solve this.

Answer 1

The difference in tension, between adjacent sections of the pull cable at the given conditions is 17.701 kN

Step-by-step explanation:

We take the cars as moving upwards such that the resultant pulling force on the car, F, along the cable is given by the relation

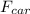`F_(car)` = Upward tension force,
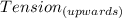`Tension_((upwards))` - Downward tension force,
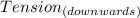`Tension_((downwards))` - Component of the weight of the car along the taut cable

The parameters given are;

Mass of car, m = 2750 kg

Angle of inclination of taut cables, θ = 35°

The upward acceleration of the car, a = 0.81 m/s²

Given that the weight is acting vertically downwards, we have;

Component of the weight of the car along the taut cable = m × g × sin(θ)

∴ Component of the weight of the car along the taut cable = 2750 × 9.81 × sin (35°) = 15473.66 N

We therefore have;

`F_(car)` =
`Tension_((upwards))` -
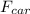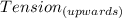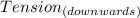`Tension_((downwards))` - 15473.66 N

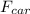`F_(car)` = m × a = 2750 × 0.81 =
`T_(upwards)` -
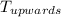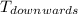`T_(downwards)` - 15473.66

∴
`Tension_((upwards))` -
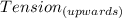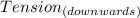`Tension_((downwards))` = 2750 × 0.81 + 15473.66 = 17701.16 N

Hence the difference in tension,
`Tension_((upwards))` -
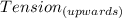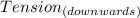`Tension_((downwards))` between adjacent sections of the pull cable if the cars are at the maximum permissible mass and are being accelerated up the incline = 17701.16 N or 17.701 kN.