Question

Question 14

For the following system of equations, determine how many solutions there are.
6x + y = -1 and -6x - 4y = 4

Answer 1

The system of equations has a one unique solution

Explanation:

To quickly determine the number of solutions of a linear system of equations, we need to express each of the equations in slope-intercept form, so we can compare their slopes, and decide:

1) if they intersect at a unique point (when the slopes are different) thus giving a one solution, or

2) if the slopes have the exact same value giving parallel lines (with no intersections, and the y-intercept is different so there is no solution), or

3) if there is an infinite number of solutions (both lines are exactly the same, that is same slope and same y-intercept)

So we write them in slope -intercept form:

First equation:

`6x+y=-1\\y=-6x-1`

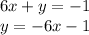
second equation:

`-6x-4y=4\\-6x=4y+4\\-6x-4=4y\\y=-(3)/(2) x-1`

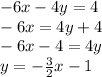
So we see that their slopes are different (for the first one slope = -6, and for the second one slope= -3/2) and then the lines must intercept in a one unique point. Therefore the system of equations has a one unique solution.