Question

BIG QUESTION, 100 POINTS

Line p contains point (6, -5) and is perpendicular to line q. The equation for line q is y = 3x + 5. Write an equation for line p.
Find the slope of line q.
Find the slope of line p. (Write the negative reciprocal of the slope you found in Part I.)
Use the point given for line p and the slope you found in Part II to write an equation for line p in point-slope form: y - y1 = m (x - x1)
Use your equation from Part III to write an equation for line p in slope-intercept form: y = mx + b. Show your work.

Answer 1

• y=3x+5

Slope of q:-

• m=3

Perpendicular line's have slopes negative reciprocal to each other

Slope of p

• -1/3

Passes through (6,-5)

Equation in point slope form

• y+5=-1/3(x-6)
• 3y+15=-x+6
• 3y=-x-9
• y=-1/3x-3

Answer 2

`\textsf{Slope of line q}: \quad 3`

`\textsf{Slope of line p}:\quad -(1)/(3)`

`\textsf{Equation of line p in slope-point form}: \quad y+5=-(1)/(3)(x-6)`

`\textsf{Equation of line p in slope-intercept form}: \quad y=-(1)/(3)x-3`

Explanation:

Slope-intercept form of a linear equation:
`y = mx + b`

(where m is the slope and b is the y-intercept)

Given:

• line q: y = 3x + 5

Therefore, the slope of line q is 3.

As line p is perpendicular to line q, the slope of line p is the negative reciprocal of the slope of line q.

Therefore, the slope of line p is -1/3

Equation of line p, using the point-slope form, the slope of -1/3 and the point (6, -5):

`\begin{aligned}y-y_1 &=m(x-x_1)\\\implies y-(-5) &=-(1)/(3)(x-6)\\y+5 &=-(1)/(3)(x-6)\end{aligned}`

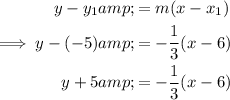
Simplify to slope-intercept form:

`\implies y=-(1)/(3)x-3`