Answer: 7.45 g of
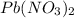 excess reagent are left over after the reaction is complete.
excess reagent are left over after the reaction is complete.
Step-by-step explanation:
To calculate the number of moles, we use the equation:
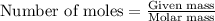
a)
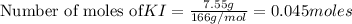
b)

The balanced chemical reaction is :
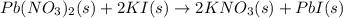
According to stoichiometry :
2 moles of
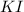 require = 1 mole of
require = 1 mole of
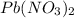
Thus 0.045 moles of
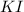 will require=
will require=
 of
of
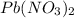
Thus
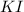 is the limiting reagent as it limits the formation of product and
is the limiting reagent as it limits the formation of product and
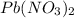 is the excess reagent as (0.045-0.0225) = 0.0225 moles are left
is the excess reagent as (0.045-0.0225) = 0.0225 moles are left
Mass of
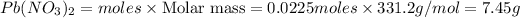
Thus 7.45 g of
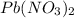 of excess reagent are left over after the reaction is complete.
of excess reagent are left over after the reaction is complete.