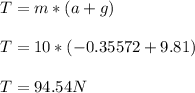Question

The block on this incline weighs 100 kg and is connected by a cable and pulley to a weight of 10 kg. If the coefficient of friction between the block and incline is o.3, the block will:

Answer 1

a. 94.54 N

b. 0.356 m/s^2

Step-by-step explanation:

Given:-

- The mass of the inclined block, M = 100 kg

- The mass of the vertically hanging block, m = 10 kg

- The angle of inclination, θ = 20°

- The coefficient of friction of inclined surface, u = 0.3

Find:-

a) The magnitude of tension in the cable

b) The acceleration of the system

Solution:-

- We will first draw a free body diagram for both the blocks. The vertically hanging block of mass m = 10 kg tends to move "upward" when the system is released.

- The block experiences a tension force ( T ) in the upward direction due the attached cable. The tension in the cable is combated with the weight of the vertically hanging block.

- We will employ the use of Newton's second law of motion to express the dynamics of the vertically hanging block as follows:

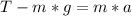`T - m*g = m*a\\\\` ... Eq 1

Where,

a: The acceleration of the system

- Similarly, we will construct a free body diagram for the inclined block of mass M = 100 kg. The Tension ( T ) pulls onto the block; however, the weight of the block is greater and tends down the slope.

- As the block moves down the slope it experiences frictional force ( F ) that acts up the slope due to the contact force ( N ) between the block and the plane.

- We will employ the static equilibrium of the inclined block in the normal direction and we have:

`N - M*g*cos ( Q )= 0\\\\N = M*g*cos ( Q )`

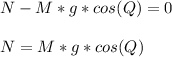
- The frictional force ( F ) is proportional to the contact force ( N ) as follows:

`F = u*N\\\\F = u*M*g *cos ( Q )`

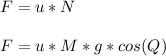
- Now we will apply the Newton's second law of motion parallel to the plane as follows:

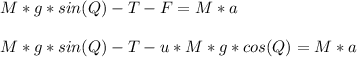`M*g*sin(Q) - T - F = M*a\\\\M*g*sin(Q) - T -u*M*g*cos(Q) = M*a\\` .. Eq2

- Add the two equation, Eq 1 and Eq 2:

`M*g*sin ( Q ) - u*M*g*cos ( Q ) - m*g = a* ( M + m )\\\\a = (M*g*sin ( Q ) - u*M*g*cos ( Q ) - m*g)/(M + m) \\\\a = (100*9.81*sin ( 20 ) - 0.3*100*9.81*cos ( 20 ) - 10*9.81)/(100 + 10)\\\\a = (-39.12977)/(110) = -0.35572 (m)/(s^2)`

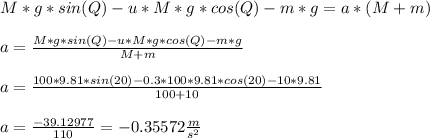
- The inclined block moves up ( the acceleration is in the opposite direction than assumed ).

- Using equation 1, we determine the tension ( T ) in the cable as follows:

`T = m* ( a + g )\\\\T = 10*( -0.35572 + 9.81 )\\\\T = 94.54 N`