Answer:
the absolute pressure in the smaller pipe = 19.63 psi
Step-by-step explanation:
Let A be the diameter of the first pipe = 3 inches
Let B be the diameter of the second pipe. = 1.5 inches
To feet (ft) ; we have
Diameter of the pipe A
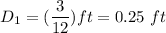
Diameter of pipe B
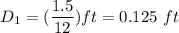
Temperature T = 120° F = (120+ 460)°R
= 580 ° R
The pressure gage to atmospheric pressure ; we have:
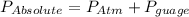
where;
atmospheric pressure = 1.47 psi
pressure gage = 20 psi
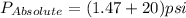
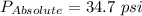
To lb/ft²; we have:
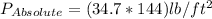
 4.998.6 fb/ft²
4.998.6 fb/ft²
The density of carbon dioxide can be calculated by using the relation

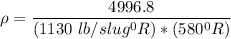

Formula for calculating cross sectional area is
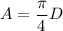
For diameter of pipe
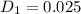
A₁ =
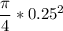
A₁ = 0.04909 ft²
For diameter of pipe
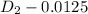
A₂
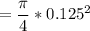
A₂ = 0.012227 ft²
Using the continuity equation to determine the velocities V₁ and V₂ respectively.
For V₁
Q = A₁V₁
V₁ = Q₁/ A₁
V₁ = 1.5/0.04909
V₁ = 30.557 ft/s
For V₂
Q = A₂V₂
V₂= Q₂/ A₂
V₂ = 1.5/0.04909
V₂ = 30.557 ft/s
Finally; using Bernoulli's Equation to the flow of the carbon dioxide from the larger pipe to the smaller pipe ; we have:
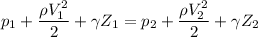
Since the pipe is horizontal then;

So;
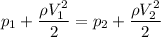
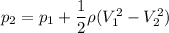
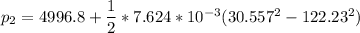
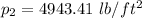
To psi;
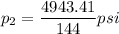
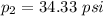 gage
gage
The absolute pressure in the smaller pipe can be calculated as:
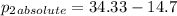
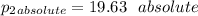
Hence, the absolute pressure in the smaller pipe = 19.63 psi