Answer:
a) The linear acceleration of the car is
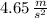 , b) The tires did 7.46 revolutions in 2.50 seconds from rest.
, b) The tires did 7.46 revolutions in 2.50 seconds from rest.
Step-by-step explanation:
a) A tire experiments a general plane motion, which is the sum of rotation and translation. The linear acceleration experimented by the car corresponds to the linear acceleration at the center of the tire with respect to the point of contact between tire and ground, whose magnitude is described by the following formula measured in meters per square second:
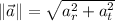
Where:
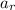 - Magnitude of the radial acceleration, measured in meters per square second.
- Magnitude of the radial acceleration, measured in meters per square second.
 - Magnitude of the tangent acceleration, measured in meters per square second.
- Magnitude of the tangent acceleration, measured in meters per square second.
Let suppose that tire is moving on a horizontal ground, since radius of curvature is too big, then radial acceleration tends to be zero. So that:


Where:
 - Angular acceleration, measured in radians per square second.
- Angular acceleration, measured in radians per square second.
 - Radius of rotation (Radius of a tire), measured in meters.
- Radius of rotation (Radius of a tire), measured in meters.
Given that
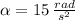 and
and
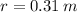 . The linear acceleration experimented by the car is:
. The linear acceleration experimented by the car is:
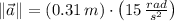
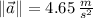
The linear acceleration of the car is
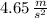 .
.
b) Assuming that angular acceleration is constant, the following kinematic equation is used:

Where:
 - Final angular position, measured in radians.
- Final angular position, measured in radians.
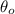 - Initial angular position, measured in radians.
- Initial angular position, measured in radians.
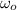 - Initial angular speed, measured in radians per second.
- Initial angular speed, measured in radians per second.
 - Angular acceleration, measured in radians per square second.
- Angular acceleration, measured in radians per square second.
 - Time, measured in seconds.
- Time, measured in seconds.
If
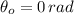 ,
,
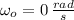 ,
,
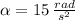 , the final angular position is:
, the final angular position is:

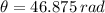
Let convert this outcome into revolutions: (1 revolution is equal to 2π radians)
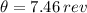
The tires did 7.46 revolutions in 2.50 seconds from rest.