Question

A firm's bonds have a maturity of 14 years with a $1,000 face value, have an 8% semiannual coupon, are callable in 7 years at $1,073.00, and currently sell at a price of $1,135.93. What are their nominal yield to maturity and their nominal yield to call? Do not round intermediate calculations. Round your answers to two decimal places.

Answer 1

YTM = 6.51%

YTC = 6.40%

Step-by-step explanation:

We need to solve using excel goal seek or bond formulas to generate the yield (interest rate) which matches the future couponb and maturity payment with the current selling price of the bond:

Present value of the coupon

`C * (1-(1+r)^(-time) )/(rate) = PV\\`

C 40.000 (1,000 x 8% / 2 payment per year)

time 28 (14 years x 2 payment per year)

rate 0.032529972 (generate using goal seek tool)

`40 * (1-(1+0.0325299719911398)^(-28) )/(0.0325299719911398) = PV\\`

PV $727.8688

Pv of the maturity (lump sum)

`(Maturity)/((1 + rate)^(time) ) = PV`

Maturity 1,000.00

time 28.00

rate 0.032529972

`(1000)/((1 + 0.0325299719911398)^(28) ) = PV`

PV 408.06

PV c $727.8688

PV m $408.0612

Total $1,135.9300

As this is a semiannual rate we multiply it by 2

0.032529972 x 2 = 0.065059944 = 6.51%

We repeat the procedure with changing the time and end-value to adjust for the callabe conditions:

`C * (1-(1+r)^(-time) )/(rate) = PV\\`

C 40.000

time 14 (7 years x 2 payment per year)

rate 0.032015131

`40 * (1-(1+0.0320151313225188)^(-14) )/(0.0320151313225188) = PV\\`

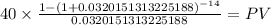
PV $445.6984

`(Maturity)/((1 + rate)^(time) ) = PV`

Maturity 1,073.00 (call price)

time 14.00

rate 0.032015131

`(1073)/((1 + 0.0320151313225188)^(14) ) = PV`

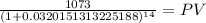
PV 690.23

PV c $445.6984

PV m $690.2316

Total $1,135.9300

Againg his will be a semiannual rate so we multiply by two:

0.032015131 x 2 = 0.064030263 = 6.40%