Question

An equilibrium mixture of the three gases in a 1.00 L flask at 350 K contains 5.35×10-2 M CH2Cl2, 0.173 M CH4 and 0.173 M CCl4. What will be the concentrations of the three gases once equilibrium has been reestablished, if 0.155 mol of CH4(g) is added to the flask?

Answer 1

[CH₂Cl₂] = 7.07x10⁻² M

[CH₄] = 0.319 M

[CCl₄] = 0.164 M

Step-by-step explanation:

The equilibrium reaction is the following:

2CH₂Cl₂(g) ⇄ CH₄(g) + CCl₄(g)

The equilibrium constant of the above reaction is:

`K = ([CH_(4)][CCl_(4)])/([CH_(2)Cl_(2)]^(2)) = (0.173 M*0.173 M)/((5.35 \cdot 10^(-2) M)^(2)) = 10.5`

When 0.155 mol of CH₄(g) is added to the flask we have the following concentration of CH₄:

`C = (\eta)/(V) = (0.155 mol)/(1.00 L) = 0.155 M`

`C_{CH_(4)} = 0.328 M`

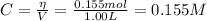
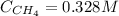
Now, the concentrations at the equilibrium are:

2CH₂Cl₂(g) ⇄ CH₄(g) + CCl₄(g)

5.35x10⁻² - 2x 0.328 + x 0.173 + x

`K = ([CH_(4)][CCl_(4)])/([CH_(2)Cl_(2)]^(2)) = ((0.328 + x)(0.173 + x))/((5.35 \cdot 10^(-2) - 2x)^(2))`

`10.5*(5.35 \cdot 10^(-2) - 2x)^(2) - (0.328 + x)*(0.173 + x) = 0`

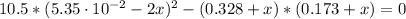
Solving the above equation for x:

x₁ = 0.076 and x₂ = -0.0086

Hence, the concentration of the three gases once equilibrium has been reestablished is:

[CH₂Cl₂] = 5.35x10⁻² - 2(-0.0086) = 7.07x10⁻² M

[CH₄] = 0.328 + (-0.0086) = 0.319 M

[CCl₄] = 0.173 + (-0.0086) = 0.164 M

We took x₂ value because the x₁ value gives a negative CH₂Cl₂ concentration.

I hope it helps you!