Question

From the mid-1960s to the early 1990s, there was a slow but steady decline in SAT scores. For example, take the Verbal SAT. The average in 1967 was about 543; by 1994, the average was down to about 499. However, the SD stayed close to 110. The drop in average has a large effect on the tails of the distribution. 0.7% 7% 7.67% 7.6%

Answer 1

Complete Question

From the mid-1960's to the early 1990's, there was a slow but steady decline in SAT scores. For example, take the Verbal SAT. The average in 1967 was about 543; by 1994, the average was down to about 499. However, the SD stayed close to 110. The drop in average has a large effect on the tails of the distribution.

Estimate the percentage of students scoring over 700 on 1967.

A 0.7%

B 7%

C 7.67%

D 7.6%

Answer:

The correct option is D

Explanation:

From the question we are told that

The average SAT score in 1967 is
`\= x_1 =543`

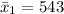
The standard deviation of score in 1967 is
`\sigma_ 1= 110`

The average SAT score in 1994 is
`\= x_2 = 499`

The standard deviation of score in 1967 is
`\sigma_ 2 = 110`

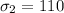
The percentage of students scoring over 700 on 1967 is mathematically represented as

`P(X > 700)`

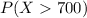
Where X is the random variable representing score of student above 700

Now normalizing the above probability we have

`P(X > 700) = P(Z > (700 - \= x_1 )/(\sigma ) )`

substituting values

`= P(Z > (700 - \= 543)/(110 ) )`

`= P(Z > 1.83 )`

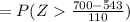
Form the normalized z table

= 0.076

= 7.6 %