Question

A company is constructing an​ open-top, square-based, rectangular metal tank that will have a volume of 49 cubic feet. What dimensions yield the minimum surface​ area? Round to the nearest tenth.

Answer 1

b = 4.6 ft

h = 2.3 ft

Explanation:

The volume of the tank is given by:

`b^2*h=49`

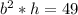
Where 'b' is the length of the each side of the square base, and 'h' is the height of the tank.

The surface area can be written as:

`A=b^2+4bh\\A=b^2+4b*({(49)/(b^2)})\\A=b^2+(196)/(b)`

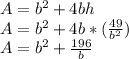
The value of b for which the derivate of the expression above is zero is the value that yields the minimum surface area:

`(dA)/(db) =0=2b-(196)/(b^2)\\2b^3=196\\b=4.61\ ft`

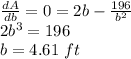
The value of h is then:

`h=(49)/(4.61^2)\\h=2.31\ ft`

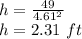
Rounded to the nearest tenth, the dimensions are b = 4.6 ft and h = 2.3 ft.