Question

g A psychic was tested for extrasensory perception (ESP). The psychic was presented with cards face down and asked to determine if each of the cards was one of four symbols: a star, cross, circle, or square. Let p represent the probability that the psychic correctly identified the symbols on the cards in a random trial. How large a sample n would you need to estimate p with margin of error 0.01 and 95% confidence?

Answer 1

The sample size should be 6157

Explanation:

Given that the margin of error (e) = ± 0.01 and the confidence (C) = 95% = 0.95.

Let us assume that the guess p = 0.25 as the value of p.

α = 1 - C = 1 - 0.95 = 0.05

`(\alpha )/(2) =(0.05)/(2)=0.025`

The Z score of α/2 is the same as the z score of 0.475 (0.5 - 0.025) which is 1.96. Therefore
`Z_(\alpha )/(2)=Z_(0.025)=1.96`

To determine the sample size n, we use the formula:

`Z_(0.025)*\sqrt{(p(1-p))/(n) }\leq e\\Substituting:\\1.96*\sqrt{(0.2(1-0.2))/(n) } \leq 0.01\\\sqrt{(0.2(0.8))/(n) }\leq (1)/(196)\\√(0.16) *196 \leq √(n)\\78.4\leq √(n)\\ 6146.56\leq n\\n=6157`

Answer 2

Explanation:

Hello!

The objective is to test ESP, for this, a psychic was presented with cards face down and asked to determine if each of the cards was one of four symbols: a star, cross, circle, square.

Be X: number of times the psychic identifies the symbols on the cards correctly is a size n sample.

p the probability that the psychic identified the symbol on the cards correctly

You have to calculate the sample size n to estimate the proportion with a confidence level of 95% and a margin of error of d=0.01

The CI for the population proportion is constructed "sample proportion" ± "margin of error" Symbolically:

p' ±
`Z_(1-\alpha /2) * (\sqrt{(p'(1-p'))/(n) } )`

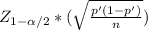
Where
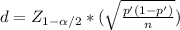`d= Z_(1-\alpha /2) * (\sqrt{(p'(1-p'))/(n) } )` is the margin of error. As you can see, the formula contains the sample proportion (it is normally symbolized p-hat, in this explanation I'll continue to symbolize it p'), you have to do the following consideration:

Every time the psychic has to identify a card he can make two choices:

"Success" he identifies the card correctly

"Failure" he does not identify the card correctly

If we assume that each symbol has the same probability of being chosen at random P(star)=P(cross)=P(circle)=P(square)= 1/4= 0.25

Let's say, for example, that the card has the star symbol.

The probability of identifying it correctly will be P(success)= P(star)= 1/4= 0.25

And the probability of not identifying it correctly will be P(failure)= P(cross) + P(circle) + P(square)= 1/4 + 1/4 + 1/4= 3/4= 0.75

So for this experiment, we'll assume the "worst case scenario" and use p'= 1/4 as the estimated probability of the psychic identifying the symbol on the card correctly.

The value of Z will be
`Z_(1-\alpha /2)= Z_(0.975)= 1.96`

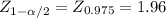
Now using the formula you have to clear the sample size:

`d= Z_(1-\alpha /2) * (\sqrt{(p'(1-p'))/(n) } )`

`(d)/(Z_(1-\alpha /2)) = \sqrt{(p'(1-p'))/(n) }`

`((d)/(Z_(1-\alpha /2)))^2 =(p'(1-p'))/(n)`

`n*((d)/(Z_(1-\alpha /2)))^2 = p'(1-p')`

`n = p'(1-p')*((Z_(1-\alpha /2))/(d))^2`

`n = (0.25*0.75)*((1.96)/(0.01))^2= 7203`

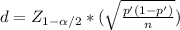
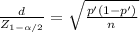
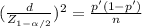
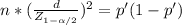
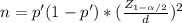
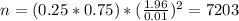
To estimate p with a margin of error of 0.01 and a 95% confidence level you have to take a sample of 7203 cards.

I hope this helps!