Question

Suppose that prices of recently sold homes in one neighborhood have a mean of $270,000 with a standard deviation of $8400. Using Chebyshev's Theorem, state the range in which at least 88.9% of the data will reside. Please do not round your answers.

Answer 1

The range in which at least 88.9% of the data will reside, ($244,800, $295,200).

Explanation:

The Chebyshev's theorem states that, if X is a random variable with mean µ and standard deviation σ then for any positive number k, we have

`P \ \geq (1-(1)/(k^(2)))`

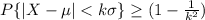
Here
`(1-(1)/(k^(2))) = 0.889`.

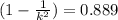Then the value of k is:

`k = [(1)/( 1-0.889)]^(1/2) = [(1)/(0.111)]^(1/2) = 3.0015\approx 3`

Then we know that,

|X - µ| ≥ kσ

⇒ µ - kσ ≤ X ≤ µ + kσ.

Here it is given that mean (µ) = $270,000 and standard deviation (σ) = $8400.

Then, the price range is given by,

`\mu - k\sigma \leq X \leq \mu + k\sigma`

`270000-(3* 8400)\leq X\leq 270000+(3* 8400)`

`244800\leq X\leq 295200`

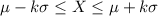
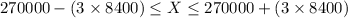
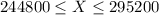
Thus, the range in which at least 88.9% of the data will reside, ($244,800, $295,200).