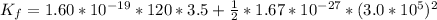Answer:
The kinetic energy is

Step-by-step explanation:
From the question we are told that
The initial speed of the proton is

The distance covered is
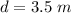
The magnitude of the electric field is

Generally the mass of a proton is
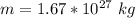
and the charge on a proton is

Now according to work energy theorem,
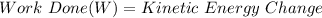
=>
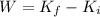
=>
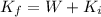
Where
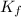 is final kinetic energy and
is final kinetic energy and
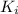 is initial kinetic energy which is mathematically represented as
is initial kinetic energy which is mathematically represented as

Now the net workdone(W) is mathematically represented as
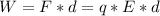
So

substituting values