The number of hits on a certain website during a one-minute interval follows a Poisson distribution with a mean rate of four hits per minute. What is the probability that there …

Question

asked Feb 8, 2021 85.6k views

1 Answer

Saad Abdullah · Answer 1 · 2021-02-15T00:50:54+0000

Answer:

86.47% probability that there is at least one hit in a 30-second period

Explanation:

In a Poisson distribution, the probability that X represents the number of successes of a random variable is given by the following formula:

$P(X = x) = (e^(-\mu)*\mu^(x))/((x)!)$

In which

x is the number of sucesses

e = 2.71828 is the Euler number

$\mu$ is the mean in the given interval.

Mean rate of four hits per minute.

This means that
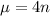$\mu = 4n$ , in which n is the number of minutes.

What is the probability that there is at least one hit in a 30-second period

30 seconds is 0.5 minutes, so
$\mu = 4*0.5 = 2$

Either the site doesn't get a hit during this period, or it does. The sum of the probabilities of these events is 1. So

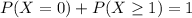
$P(X = 0) + P(X \geq 1) = 1$

We want
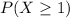
$P(X \geq 1)$

Then

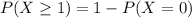
$P(X \geq 1) = 1 - P(X = 0)$

In which

$P(X = x) = (e^(-\mu)*\mu^(x))/((x)!)$

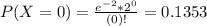
P(X = 0) = (e^(-2)*2^(0))/((0)!) = 0.1353

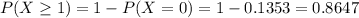
$P(X \geq 1) = 1 - P(X = 0) = 1 - 0.1353 = 0.8647$

86.47% probability that there is at least one hit in a 30-second period