Question

g Suppose a uniform slender rod has length L and mass m. The moment of inertia of the rod about about an axis that is perpendicular to the rod and that passes through its center of mass is given by Icm=112mL2. Find Iend, the moment of inertia of the rod with respect to a parallel axis through one end of the rod.

Answer 1

`I_e = (1)/(3)*m*L^2`

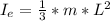
Step-by-step explanation:

Solution:-

- Here we are given the moment of inertia of a uniform slender rod with mass ( m ) and length ( L ). The thickness / radius / diameter of the rod is considered to be insignificant.

- The moment of inertia ( Ir ) of a rod with an axis perpendicular to it at its center is given as:

`I_r = (1)/(12)*m*L^2`

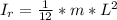
- We are to determine the moment of inertia of the rod at any one of its ends using the parallel axis theorem.

- The theorem is mostly used to translate the pivotal axis to any point on the mass or in space. With respect to that point the moment of inertia is determined using the parallel axis theorem. The moment of inertia of the object at its center of mass must be known to apply the theorem.

- The theorem is expressed as:

`I_e = I_r + m*d^2`

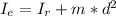
Here,

d: Is the distance between the center of mass and the arbitrary point.

- Since we are asked to determine the moment of inertial at one of the rod's ends. We can evaluate the distance " d " from its center of mass to its end. The center lies at " L / 2 " distance from either of its ends. Hence, d = L / 2.

- We will plug in the parameters in the theorem and evaluate:

`I_e = (1)/(12)*m*L^2 + m*[(L)/(2) ]^2 \\\\I_e = (1)/(12)*m*L^2 + m*(L^2)/(4) \\\\I_e = m*L^2 * [ (1)/(12)+ (3)/(12) ] = m*L^2 *(4)/(12) \\\\I_e = (1)/(3)*m*L^2`