Question

All applicants for admission to graduate study in business are given a standardized test. Scores are normally distributed with a mean of 460 and standard deviation of 80. What fraction of applicants would you expect to have scores of 600 or above

Answer 1

The probability that applicants would you expect to have scores of 600 or above = 0.0401 or 4%

Explanation:

Explanation:-

Let "x" Scores are normally distributed

Given mean of the Population = 460

standard deviation of the population = 80

Let X = 600

`Z = (x -mean)/(S.D) = (600-460)/(80) =1.75`

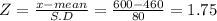
The probability that applicants would you expect to have scores of 600 or above

P( X≥600) = P( Z≥ 1.75)

= 1- P( Z≤1.75)

= 1- ( 0.5 + A(1.75)

= 1- 0.5 - A(1.75)

= 0.5 - 0.4599 (from Normal table)

= 0.0401

The probability that applicants would you expect to have scores of 600 or above = 0.0401 or 4%