Answer:
7.5 m/s
Step-by-step explanation:
We can find its velocity when it reaches the buoy by applying one of Newton's equations of motion:
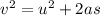
where v = final velocity
u = initial velocity
a = acceleration
s = distance traveled
From the question:
u = 28 m/s
a = -4
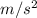
s = 91 m
Therefore:

The velocity of the boat when it reaches the buoy is 7.5 m/s.