Question

An aluminum rod is designed to break when it is under a tension of 600 N. One end of the rod is connected to a motor and a 12-kg spherical object is attached to the other end. When the motor is turned on, the object moves in a horizontal circle with a radius of 5.78 m. If the speed of the motor is continuously increased, at what speed will the rod break

Answer 1

17 m/s

Step-by-step explanation:

Given:

Tension = 600 N

Mass of object, M= 12 kg

Radius, r = 5.78 m

Required:

Find the speed the rod will break

Here, the motor is continuously increased. To find the speed the rod will break (speed of centripetal force), we have:

Tension = Centripetal force

Where centripetal force =
`(mv^2)/(r)`

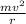
Therefore,

`T = (mv^2)/(r)`

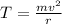
Make v subject of the formula:

`v = \sqrt{(T*r)/(m)}`

`= \sqrt{(600*5.78)/(12)}`

`= \sqrt{(3468)/(12)`

`= √(289)`

`= 17 m/s`

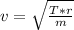
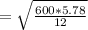
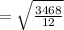
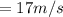
Speed the rod will break is 17 m/s.