Answer:
the velocity of the cylinder after dropping an additional 1.28 m is 1.15 m/s
Step-by-step explanation:
Using the work energy system
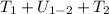
The initial kinetic energy
 is ;
is ;
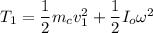
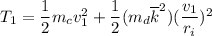
where;
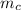 = mass of the cylinder = 7.7 kg
= mass of the cylinder = 7.7 kg
 initial velocity of the cylinder = 0.49 m/s
initial velocity of the cylinder = 0.49 m/s
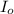 = moment of inertia of the drum about O
= moment of inertia of the drum about O
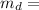 mass of the drum = 10.5 kg
mass of the drum = 10.5 kg
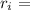 radius of gyration = 0.3 m
radius of gyration = 0.3 m
 = angular velocity of the drum
= angular velocity of the drum
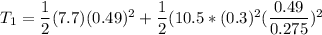

The final kinetic energy is also calculated as:
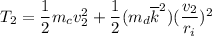
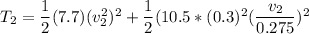
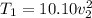
Similarly, The workdone by all the forces on the cylinder can be expressed as:
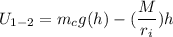
where;
g = acceleration due to gravity
h = drop in height of the cylinder
M = frictional moment at O

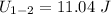
Finally, using the work energy application;
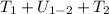
2.426 + 11.04 = 10.10
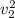
13.466 = 10.10
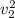
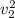 =
=
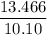
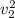 = 1.333
= 1.333
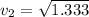
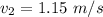
Thus, the velocity of the cylinder after dropping an additional 1.28 m is 1.15 m/s