Question

Each leg of a 45°-45°-90° triangle measures 12 cm. Triangle X Y Z is shown. Angle X Y Z is a right angle and angles Y Z X and Z X Y are 45 degrees. The lengths of sides Z Y and Y X are 12 centimeters. What is the length of the hypotenuse? 6 cm 6 StartRoot 2 EndRoot cm 12 cm 12 StartRoot 2 EndRoot cm

Answer 1

Length of hypotenuse
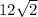`12\sqrt2` cm.

Explanation:

We are given with a right angled triangle which has angles 45°-45°-90° and sides as 12 cm each.

Following labeling of dimensions is provided:

`\angle XYZ = 90^\circ\\\angle YZX = 45^\circ\\\angle ZXY = 45^\circ`

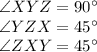
Sides:

ZY = 12 cm

YX = 12 cm

Please refer to the image attached as well.

To find: The hypotenuse, XZ = ?

It is well known that if the triangle is a right angled triangle, the pythagorean theorem holds well. As per the theorem:

`\text{Hypotenuse}^(2) = \text{Base}^(2) + \text{Height}^(2)\\`

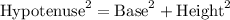
Here, Base is ZY = 12 cm

Height, YZ = 12 cm

And Hypotenuse XZ is to be calculated.

Putting the values:

`XZ^2=12^2+12^2\\\Rightarrow XZ^2=144+144\\\Rightarrow XZ=√(144+144)\\\Rightarrow XZ=√(288)\\\Rightarrow XZ=12√(2)\ cm`

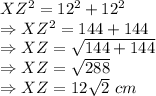
So, the answer is Hypotenuse, XZ =
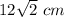`12√(2)\ cm`.