Answer:
The numbers of doors that will have no blemishes will be about 6065 doors
Explanation:
Let the number of counts by the worker of each blemishes on the door be (X)
The distribution of blemishes followed the Poisson distribution with parameter
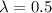 / door
/ door
The probability mass function on of a poisson distribution Is:
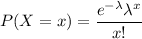

The probability that no blemishes occur is :
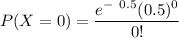

P(X=0) = 0.6065
Assume the number of paints on the door by q = 10000
Hence; the number of doors that have no blemishes is = qp
=10,000(0.6065)
= 6065