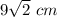Question

The hypotenuse of a 45°-45°-90° triangle measures 18 cm.

A right triangle is shown. The other 2 angle measures are 45 degrees. The length of the hypotenuse is 18 centimeters.

What is the length of one leg of the triangle?

Answer 1

answer is B 9 root 2 cm

Explanation:

got it right on edg 2020-2021

Answer 2

Length of leg of triangle =
`9\sqrt2\ cm`

Explanation:

We are given a 45°-45°-90° triangle with hypotenuse measuring 18 cm.

Let us assume the following labeling of the diagram, as attached in the answer area.

`\angle XYZ =90^\circ\\\angle YXZ =45^\circ\\\angle ZXY =45^\circ\\\\Hypotenuse, XZ = 18 cm`

The two angles here are equal to 45° so two sides of the triangle opposite to the equal angles will also be equal to each other i.e. it is an isosceles triangle.

i.e. The sides XY and YZ will be equal.

Let XY = YZ = x cm

It is known that in a right angled triangle, pythagorean theorem holds well.

As per pythagoream theorem:

`\text{Hypotenuse}^(2) = \text{Base}^(2) + \text{Height}^(2)`

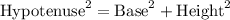
Putting the values:

`\text{XZ}^(2) = \text{YZ}^(2) + \text{XY}^(2)\\\Rightarrow 18^2 = x^(2) +x^(2) \\\Rightarrow 2x^(2) = 18^2\\\Rightarrow 2x^(2) = 324\\\Rightarrow x^(2) = 162\\\Rightarrow x = √(2 * 81)\\\Rightarrow x = 9\sqrt2\ cm`

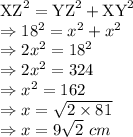
So, the length of leg of triangle =
`9\sqrt2\ cm`