Question

g A life insurance salesman sells on the average 3 life insurance policies per week. Calculate the probability that in a given week he will sell 2 or more policies but less 4 policies.

Answer 1

44.80% probability that in a given week he will sell 2 or more policies but less than 4 policies.

Explanation:

In a Poisson distribution, the probability that X represents the number of successes of a random variable is given by the following formula:

`P(X = x) = (e^(-\mu)*\mu^(x))/((x)!)`

In which

x is the number of sucesses

e = 2.71828 is the Euler number

`\mu` is the mean in the given interval.

A life insurance salesman sells on the average 3 life insurance policies per week.

This means that
`\mu = 3`

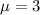
Calculate the probability that in a given week he will sell 2 or more policies but less 4 policies.

`P(2 \leq X < 4) = P(X = 2) + P(X = 3)`

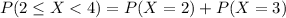
In which

`P(X = x) = (e^(-\mu)*\mu^(x))/((x)!)`

`P(X = 2) = (e^(-3)*3^(2))/((2)!) = 0.2240`

`P(X = 3) = (e^(-3)*3^(3))/((3)!) = 0.2240`

`P(2 \leq X < 4) = P(X = 2) + P(X = 3) = 0.2240 + 0.2240 = 0.4480`

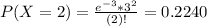
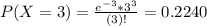
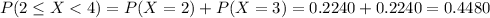
44.80% probability that in a given week he will sell 2 or more policies but less than 4 policies.