Question

The top and bottom margins of a poster are each 15 cm and the side margins are each 10 cm. If the area of printed material on the poster is fixed at 2400 cm2, find the dimensions of the poster with the smallest area.

Answer 1

the dimension of the poster = 90 cm length and 60 cm width i.e 90 cm by 60 cm.

Explanation:

From the given question.

Let p be the length of the of the printed material

Let q be the width of the of the printed material

Therefore pq = 2400 cm ²

q =
`(2400 \ cm^2)/(p)`

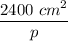
To find the dimensions of the poster; we have:

the length of the poster to be p+30 and the width to be
`(2400 \ cm^2)/(p) + 20`

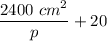
The area of the printed material can now be:
`A = (p+30)((2400 )/(p) + 20)`

=
`2400 +20 p +(72000)/(p)+600`

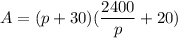
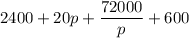
Let differentiate with respect to p; we have

`(dA)/(dp)= 20 - (72000)/(p^3)`

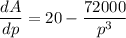
Also;

`(d^2A)/(dp^2)= (144000)/(p^3)`

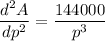
For the smallest area
`(dA)/(dp )=0`

`20 - (72000)/(p^2)=0`

`p^2 = (72000)/(20)`

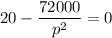
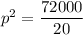
p² = 3600

p =√3600

p = 60

Since p = 60 ; replace p = 60 in the expression q =
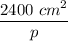`(2400 \ cm^2)/(p)` to solve for q;

q =
`(2400 \ cm^2)/(p)`

q =
`(2400 \ cm^2)/(60)`

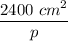
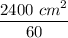
q = 40

Thus; the printed material has the length of 60 cm and the width of 40cm

the length of the poster = p+30 = 60 +30 = 90 cm

the width of the poster =
`(2400 \ cm^2)/(p) + 20` =
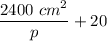`(2400 \ cm^2)/(60) + 20` = 40 + 20 = 60

Hence; the dimension of the poster = 90 cm length and 60 cm width i.e 90 cm by 60 cm.