Question

What is an equation of the line that passes through the points (−3,−4) and (-4, -6)

Answer 1

`\text{Given that,}\\\\(x_1,y_1) =(-3,-4)~~ \text{and}~~ (x_2,y_2) = (-4,-6)\\\\\text{Slope,}~m = (y_2 -y_1)/(x_2 -x_1) = (-6+4)/(-4+3) = (-2)/(-1) =2\\ \\\text{Equation of line,}\\\\~~~~~y-y_1 = m(x-x_1)\\\\\implies y+4=2(x+3)\\\\\implies y =2x+6-4\\ \\\implies y= 2x+2`

Answer 2

• 
  `\Large\boxed{\sf{y=2x+2}}`

Explanation:

Use the slope formula.

SLOPE FORMULA:


`\Rightarrow: \sf{(y_2-y_1)/(x_2-x_1)}`

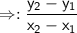
• y2=(-6)
• y1=(-4)
• x2=(-4)
• y1=(-3)

`:\Longrightarrow \sf{(-6-\left(-4\right))/(-4-\left(-3\right))}`

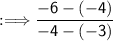
Solve.

`\sf{(-6-\left(-4\right))/(-4-\left(-3\right))=(-6+4)/(-4+3)=(-2)/(-1)=2}`

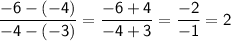
The slope is 2.

Use the slope-intercept form.

SLOPE-INTERCEPT FORM:

`\sf{y=mx+b}`

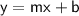
• X=slope
• B=y-intercept.
• The y-intercept is 2.

y=2x+2

• Therefore, the final answer is y=2x+2.

I hope this helps, let me know if you have any questions.