Answer:
Explanation:
Use the slope formula.
SLOPE FORMULA:
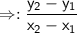
- y2=(-6)
- y1=(-4)
- x2=(-4)
- y1=(-3)
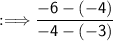
Solve.
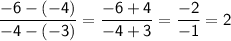
The slope is 2.
Use the slope-intercept form.
SLOPE-INTERCEPT FORM:
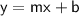
- X=slope
- B=y-intercept.
- The y-intercept is 2.
y=2x+2
- Therefore, the final answer is y=2x+2.
I hope this helps, let me know if you have any questions.