Answer:
The probability that a defective rod can be salvaged = 0.50
Explanation:
Given that:
A machine shop produces heavy duty high endurance 20-inch rods
On occasion, the machine malfunctions and produces a groove or a chisel cut mark somewhere on the rod.
If such defective rods can be cut so that there is at least 15 consecutive inches without a groove.
Then; The defective rod can be salvaged if the groove lies on the rod between 0 and 5 inches i.e ( 20 - 15 )inches
Now:
P(X ≤ 5) =
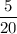
= 0.25
P(X ≥ 15) =
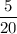
= 0.25
The probability that a defective rod can be salvaged = P(X ≤ 5) + P(X ≥ 15)
= 0.25+0.25
= 0.50
∴ The probability that a defective rod can be salvaged = 0.50