Complete Question
A recent CBS News survey reported that 64% of adults felt the U.S. Treasury should continue making pennies. Suppose we select a sample of 18 adults.
a-1. How many of the 18 would we expect to indicate that the Treasury should continue making pennies
a-2) What is the standard deviation?
a-3) What is the likelihood that exactly 3 adults would indicate the Treasury should continue making pennies?
Answer:
a-1
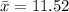
a-2
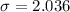
a-3

Explanation:
From the question we are told that
The sample size is

The proportion of adult that felt the U.S. Treasury should continue making pennies is p = 0.64
The proportion of adult that feel otherwise is
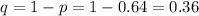
The mean is mathematically evaluated as
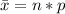
substituting values

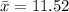
The standard deviation is mathematically represented as
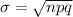
substituting values
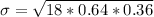
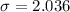
The likelihood that 3 adult would indicate the Treasury should continue making pennies is mathematically evaluated as

Now
![\left n} \atop \right. C_3 = (n! )/([n-3] ! 3!)](https://img.qammunity.org/2021/formulas/mathematics/college/a83g36hmryobhahlbpj6e970atds590md5.png)
substituting values
![\left n} \atop \right. C_3 = (18! )/([15] ! 3!)](https://img.qammunity.org/2021/formulas/mathematics/college/vs3wdeesntpxlyt0wjbwcpaez8l3m0qmtp.png)
![\left n} \atop \right. C_3 = (18 * 17 * 16 * 15! )/([15] ! (3 *2 *1 ))](https://img.qammunity.org/2021/formulas/mathematics/college/w0j1j220oy508p1g97fy0yk9nm53hpp2gx.png)

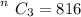
So