Question

To get up on the roof, a person (mass 69.0 kg) places a 6.40 m aluminum ladder (mass 11.0 kg) against the house on a concrete pad with the base of the ladder 2.00 m from the house. The ladder rests against a plastic rain gutter, which we can assume to be frictionless. The center of mass of the ladder is 2 m from the bottom. The person is standing 3 m from the bottom. What are the magnitudes (in N) of the forces on the ladder at the top and bottom

Answer 1

N = 243.596 N ≈ 243.6 N

Step-by-step explanation:

mass of person = 69 kg ( M )

mass of aluminium ladder = 11 kg ( m )

length of ladder = 6.4 m ( l )

base of ladder = 2 m from the house (d )

center of mass of ladder = 2 m from the bottom of ladder

person on ladder standing = 3 m from bottom of ladder

Calculate the magnitudes of the forces at the top and bottom of the ladder

The net torque on the ladder = o ( since it is at equilibrium )

assuming: the weight of the person( mg) acting at a distance x along the ladder. the weight of the ladder ( mg) acting halfway along the ladder and the reaction N acting on top of the ladder

X = l/2

x = 6.4 / 2 = 3.2

find angle formed by the ladder

cos ∅ = d/l

∅ =
`cos^{-1]` 2/6.4 =
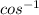`cos^(-1)`0.3125 ≈ 71.79⁰

remember the net torque around is = zero

to calculate the magnitude of forces on the ladder we apply the following formula

`N = (mg(dcosteta)+ Mgxcosteta)/(lsinteta)`

m = 11 kg, M = 69 kg, l = 6.4 , x = 3, teta( ∅ )= 71.79⁰, g = 9.8

back to equation N =
`(11*9.8(2*cos71.79)+ 69*9.8*3* cos71.79)/(6.4sin71.79)`

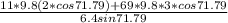
N = (67.375 + 633.938) / 2.879

N = 243.596 N ≈ 243.6 N