Answer:
v = 46.99 m/s
Step-by-step explanation:
The velocity of the ball just before it touches the ground, is given by the following formula:
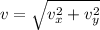 (1)
(1)
vx: horizontal component of the velocity
vy: vertical component of the velocity
The vertical component vy is calculated by using the following formula:
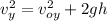 (2)
(2)
vy: final velocity
voy: initial vertilal velocity = 0m/s (because it is a semi parabolic motion)
g: gravitational acceleration = 9.8 m/s^2
h: height = 1.60m
You replace the values of the parameters in the equation (2):
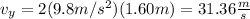
vx is calculated by using the information about the horizontal range of the ball:
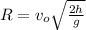 (3)
(3)
R: horizontal range of the ball = 20.0 m
You solve the previous equation for vo, the initial horizontal velocity:
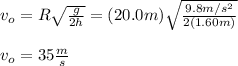
The horizontal component of the velocity is constant in the complete trajectory, hence, you have that
vx = vo = 35 m/s
Finally, you replace the values of vx and vy in the equation (1):
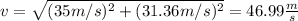
The velocity of the ball just before it touches the ground is 46.99 m/s