Answer:
Step-by-step explanation:
The velocity at the inlet and exit of the control volume are same
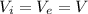
Calculate the inlet and exit velocity of water jet
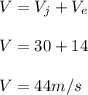
The conservation of mass equation of steady flow

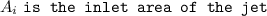
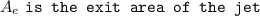
since inlet and exit velocity of water jet are equal so the inlet and exit cross section area of the jet is equal
The expression for thickness of the jet
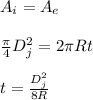
R is the radius
t is the thickness of the jet
D_j is the diameter of the inlet jet

(b)
![R-x=\rho(AV_r)[-(V_i)+(V_c)\cos 60^o]\\\\=\rho(V_j+V_c)A[-(V_i+V_c)+(V_i+V_c)\cos 60^o]\\\\=\rho(V_j+V_c)((\pi)/(4)D_j^2 )[V_i+V_c](\cos60^o-1)]](https://img.qammunity.org/2021/formulas/physics/college/dsiowu3uwsqugqxtpke3trkcn8s3k8yg03.png)
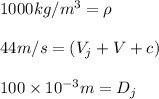
![R_x=[1000*(44)(\pi)/(4) (10*10^(-3))^2[(44)(\cos60^o-1)]]\\\\=-7603N](https://img.qammunity.org/2021/formulas/physics/college/w9xbsn9p1occuip2ffwoyxa7qoqwvxdyst.png)
The negative sign indicate that the direction of the force will be in opposite direction of our assumption
Therefore, the horizontal force is -7603N