Question

A ball is thrown upward from the ground with an initial speed of 19.2 m/s; at the same instant, another ball is dropped from a building 18 m high. After how long will the balls be at the same height above the ground?

Answer 1

0.938 seconds

Step-by-step explanation:

For the ball thrown upwards, we use the formula below to solve it:

`s = ut - (1)/(2)gt^2`

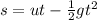
where s = distance moved

u = initial speed = 19.2 m/s

t = time taken

g = acceleration due to gravity = 9.8
`m/s^2`

Let x be the height at which both balls are level, this means that:

=>
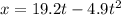`x = 19.2t - 4.9t^2`________(1)

For the ball dropped downwards, we use the formula below:

`s = ut + (1)/(2)gt^2`

u = 0 m/s

At the point where both balls are level:

s = 18 - x

=>
`18 - x = 0 + 4.9t^2`

=>
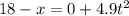
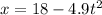`x = 18 - 4.9t^2`__________(2)

Equating both (1) and (2):

`19.2t - 4.9t^2 = 18 - 4.9t^2\\\\=> 19.2t = 18\\\\t = 18/19.2 = 0.938 secs`

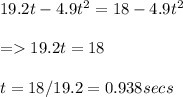
They will be level after 0.938 seconds