Question

I need help on this one please

Answer 1

The surface area of the triangular prism is
`A=122\:in^2`.

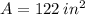Explanation:

The surface area of any prism is the total area of all its sides and faces. A triangular prism has three rectangular sides and two triangular faces.

An equilateral triangle is a triangle with all three sides of equal length.

To find the surface area, the area of each face is calculated and then add these areas together.

The formula
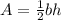`A=(1)/(2) bh` is used to find the area of the triangular faces, where A = area, b = base, and h = height.

The formula
`A=lw` is used to find the area of the three rectangular side faces, where A = area, l = length, and w = width.

The surface area of the triangular faces is:

`A=(1)/(2) (4)(3.5)+(1)/(2) (4)(3.5)\\A=2\cdot \:4\cdot \:3.5\cdot (1)/(2)\\A=1\cdot \:4\cdot \:3.5\\A=14\:in^2`

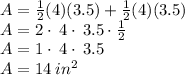
The surface area of the three rectangular side faces is:

`A=4\cdot9+4\cdot9+4\cdot9=108\:in^2`

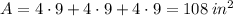
The surface area of the triangular prism is
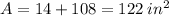`A=14+108=122\:in^2`.