Question

A helium nucleus (charge = 2e, mass = 6.63 10-27 kg) traveling at 6.20 105 m/s enters an electric field, traveling from point circled A, at a potential of 1.50 103 V, to point circled B, at 4.00 103 V. What is its speed at point circled B?

Answer 1

`v_B=3.78* 10^5\ m/s`

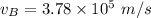
Step-by-step explanation:

It is given that,

Charge on helium nucleus is 2e and its mass is
`6.63* 10^(-27)\ kg`

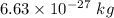
Speed of nucleus at A is
`v_A=6.2* 10^5\ m/s`

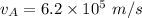
Potential at point A,
`V_A=1.5* 10^3\ V`

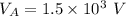
Potential at point B,
`V_B=4* 10^3\ V`

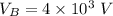
We need to find the speed at point B on the circle. It is based on the concept of conservation of energy such that :

increase in kinetic energy = increase in potential×charge

`(1)/(2)m(v_A^2-v_B^2)=(V_B-V_A)q\\\\(1)/(2)m(v_A^2-v_B^2)={(4* 10^3-1.5* 10^3)}* 2* 1.6* 10^(-19)=8* 10^(-16)\\\\v_A^2-v_B^2=(2* 8* 10^(-16))/(6.63* 10^(-27))\\\\v_A^2-v_B^2=2.41* 10^(11)\\\\v_B^2=(6.2* 10^5)^2-2.41* 10^(11)\\\\v_B=3.78* 10^5\ m/s`

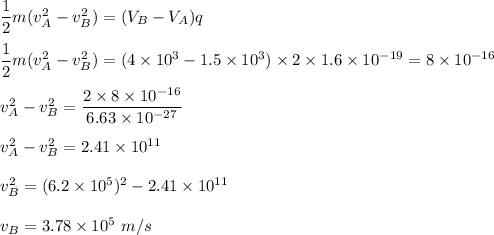
So, the speed at point B is
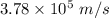`3.78* 10^5\ m/s`.