Question

A researcher records the repair cost for 8 randomly selected refrigerators. A sample mean of $57.89 and standard deviation of $23.69 are subsequently computed. Determine the 95% confidence interval for the mean repair cost for the refrigerators. Assume the population is approximately normal. Step 1 of 2 : Find the critical value that should be used in constructing the confidence interval. Round your answer to three decimal places.

Answer 1

The question is incomplete! the complete question along with answer and step by step explanation is provided below.

Question:

A researcher records the repair cost for 8 randomly selected refrigerators. A sample mean of $57.89 and standard deviation of $23.69 are subsequently computed. Determine the 95% confidence interval for the mean repair cost for the refrigerators. Assume the population is approximately normal.

Step 1 of 2 : Find the critical value that should be used in constructing the confidence interval. Round your answer to three decimal places.

Step 2 of 2 : Construct the 95% confidence interval. Round your answer to two decimal places.

Given Information:

Sample mean repair cost = $57.89

Sample standard deviation = σ = $23.69

Sample size = 8

Confidence level = 95%

Required Information:

step 1: critical value = ?

step 2: 95% confidence interval = ?

Answer:

step 1: critical value = 2.365

step 2: 95% confidence interval = ($38.08, $77.70)

Explanation:

Since the sample size is less than 30 and the standard deviation of the population is also unknown therefore, we can use the t-distribution to find the required confidence interval.

The confidence interval is given by

`CI = \bar{x} \pm MoE\\\\`

Where
`\bar{x}` is the mean repair cost and MoE is the margin of error that is given by

`$ MoE = t_(\alpha/2)((s)/(√(n) ) ) $ \\\\`

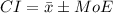
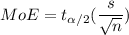
Where n is the sample size, s is the sample standard deviation, and
`t_(\alpha/2)` is the t-score corresponding to 95% confidence level.

The t-score corresponding to 95% confidence level is

Significance level = 1 - 0.95 = 0.05/2 = 0.025

Degree of freedom (DoF) = n - 1 = 8 - 1 = 7

From the t-table at α = 0.025 and DoF = 7

t-score = 2.365

Therefore, the critical value that should be used in constructing the confidence interval is 2.365

`MoE = 2.365\cdot (23.69)/(√(8) ) \\\\MoE = 2.365\cdot 8.3756\\\\MoE = 19.808 \\\\`

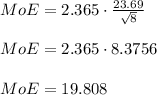
So the required 95% confidence interval is

`CI = \bar{x} \pm MoE\\\\CI = 57.89 \pm 19.808\\\\CI = 57.89 - 19.808 \: and \: 57.89 + 19.808\\\\CI = \$38.08 \: and \:\:\$77.70\\`

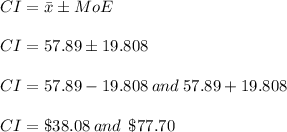
Therefore, we are 95% confident that the mean repair cost for the refrigerators is within the range of ($38.08, $77.70)