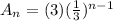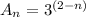Question

If the fifth term in a geometric sequence is 1∕27 and the common ratio is 1∕3, find the explicit formula of the sequence.

Answer 1

Explicit formula will be
`A_n=3^((2-n))`

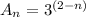
Explanation:

Explicit formula for a geometric sequence is given by the formula,

`A_n=a(r)^(n-1)`

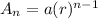
Here
`A_n` is the nth term of the sequence

a = first term of the sequence

n = number of term

Since 5th term of a geometric sequence is

`A_5` =
`(1)/(27)`

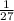
First term of the sequence 'a'=
`(1)/(3)`

By substituting these values in the explicit formula,

`(1)/(27)=a((1)/(3))^(5-1)`

`(1)/(27) =a((1)/(3))^4`

a =
`((1)/(27))/((1)/(81))`

a =
`(81)/(27)`

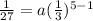
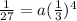
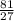
a = 3

Therefore, explicit formula of this sequence will be,

`A_n=(3)((1)/(3))^(n-1)`

`A_n=(3)(3)^((-n+1))`

`A_n=3^((2-n))`