Question

Mileage tests were conducted on a randomly selected sample of 100 newly developed automobile tires. The results showed that the mean tread life was 50,000 miles, with a standard deviation of 3,500 miles. What is the best estimate of the mean tread life in miles for the entire population of these tires?

Answer 1

The best estimate of the mean of the population is 50,000 miles, which is the sample mean.

To make a better inference, we know that the 95% confidence interval for the mean is (49,306; 50,694).

Explanation:

The unbiased point estimation for the population mean tread life is the sample mean (50,000 miles), as it is the only information we have.

Although, knowing the standard deviation, we can calculate a confidence interval to make a stronger inference.

We calculate a 95% confidence interval for the mean.

The population standard deviation is not known, so we have to estimate it from the sample standard deviation and use a t-students distribution to calculate the critical value.

The sample mean is M=50000.

The sample size is N=100.

When σ is not known, s divided by the square root of N is used as an estimate of σM:

`s_M=(s)/(√(N))=(3500)/(√(100))=(3500)/(10)=350`

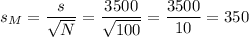
The degrees of freedom for this sample size are:

`df=n-1=100-1=99`

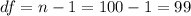
The t-value for a 95% confidence interval and 99 degrees of freedom is t=1.98.

The margin of error (MOE) can be calculated as:

`MOE=t\cdot s_M=1.98 \cdot 350=694.48`

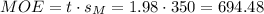
Then, the lower and upper bounds of the confidence interval are:

`LL=M-t \cdot s_M = 50000-694.48=49306\\\\UL=M+t \cdot s_M = 50000+694.48=50694`

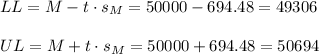
The 95% confidence interval for the mean is (49306, 50694).